Stack and Queue
前言
Java里有一个叫做Stack的类,却没有叫做Queue的类(它是个接口名字)。当需要使用栈时,Java已不推荐使用Stack,而是推荐使用更高效的ArrayDeque;既然Queue只是一个接口,当需要使用队列时也就首选ArrayDeque了(次选是LinkedList)。
总体介绍
要讲栈和队列,首先要讲Deque接口。Deque的含义是“double ended queue”,即双端队列,它既可以当作栈使用,也可以当作队列使用。下表列出了Deque与Queue相对应的接口:
| Queue Method | Equivalent Deque Method | 说明 |
|---|---|---|
add(e) |
addLast(e) |
向队尾插入元素,失败则抛出异常 |
offer(e) |
offerLast(e) |
向队尾插入元素,失败则返回false |
remove() |
removeFirst() |
获取并删除队首元素,失败则抛出异常 |
poll() |
pollFirst() |
获取并删除队首元素,失败则返回null |
element() |
getFirst() |
获取但不删除队首元素,失败则抛出异常 |
peek() |
peekFirst() |
获取但不删除队首元素,失败则返回null |
下表列出了Deque与Stack对应的接口:
| Stack Method | Equivalent Deque Method | 说明 |
|---|---|---|
push(e) |
addFirst(e) |
向栈顶插入元素,失败则抛出异常 |
| 无 | offerFirst(e) |
向栈顶插入元素,失败则返回false |
pop() |
removeFirst() |
获取并删除栈顶元素,失败则抛出异常 |
| 无 | pollFirst() |
获取并删除栈顶元素,失败则返回null |
peek() |
peekFirst() |
获取但不删除栈顶元素,失败则抛出异常 |
| 无 | peekFirst() |
获取但不删除栈顶元素,失败则返回null |
上面两个表共定义了Deque的12个接口。添加,删除,取值都有两套接口,它们功能相同,区别是对失败情况的处理不同。一套接口遇到失败就会抛出异常,另一套遇到失败会返回特殊值(false或null)。除非某种实现对容量有限制,大多数情况下,添加操作是不会失败的。虽然Deque的接口有12个之多,但无非就是对容器的两端进行操作,或添加,或删除,或查看。明白了这一点讲解起来就会非常简单。
ArrayDeque和LinkedList是Deque的两个通用实现,由于官方更推荐使用AarryDeque用作栈和队列,加之上一篇已经讲解过LinkedList,本文将着重讲解ArrayDeque的具体实现。
从名字可以看出ArrayDeque底层通过数组实现,为了满足可以同时在数组两端插入或删除元素的需求,该数组还必须是循环的,即循环数组(circular array),也就是说数组的任何一点都可能被看作起点或者终点。ArrayDeque是非线程安全的(not thread-safe),当多个线程同时使用的时候,需要程序员手动同步;另外,该容器不允许放入null元素。
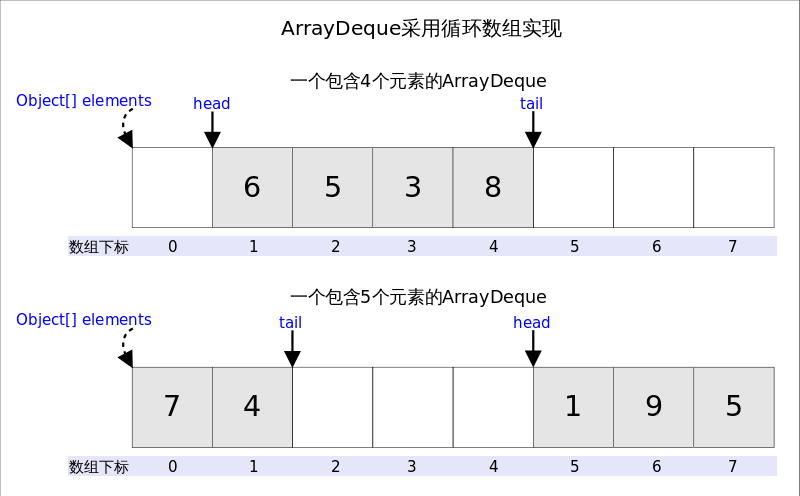
上图中我们看到,head指向首端第一个有效元素,tail指向尾端第一个可以插入元素的空位。因为是循环数组,所以head不一定总等于0,tail也不一定总是比head大。
方法剖析
addFirst()
addFirst(E e)的作用是在Deque的首端插入元素,也就是在head的前面插入元素,在空间足够且下标没有越界的情况下,只需要将elements[--head] = e即可。
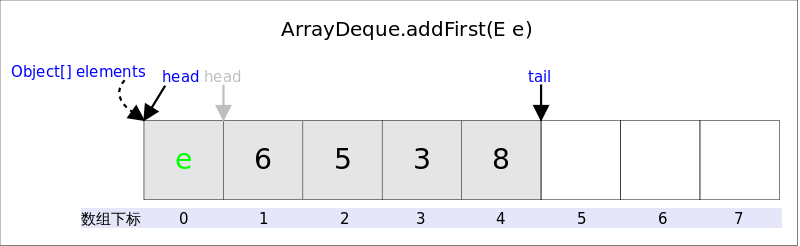
实际需要考虑:1.空间是否够用,以及2.下标是否越界的问题。上图中,如果head为0之后接着调用addFirst(),虽然空余空间还够用,但head为-1,下标越界了。下列代码很好的解决了这两个问题。
//addFirst(E e)
public void addFirst(E e) {
if (e == null)//不允许放入null
throw new NullPointerException();
elements[head = (head - 1) & (elements.length - 1)] = e;//2.下标是否越界
if (head == tail)//1.空间是否够用
doubleCapacity();//扩容
}
上述代码我们看到,空间问题是在插入之后解决的,因为tail总是指向下一个可插入的空位,也就意味着elements数组至少有一个空位,所以插入元素的时候不用考虑空间问题。
下标越界的处理解决起来非常简单,head = (head - 1) & (elements.length - 1)就可以了,这段代码相当于取余,同时解决了head为负值的情况。因为elements.length必需是2的指数倍,elements - 1就是二进制低位全1,跟head - 1相与之后就起到了取模的作用,如果head - 1为负数(其实只可能是-1),则相当于对其取相对于elements.length的补码。
下面再说说扩容函数doubleCapacity(),其逻辑是申请一个更大的数组(原数组的两倍),然后将原数组复制过去。过程如下图所示:
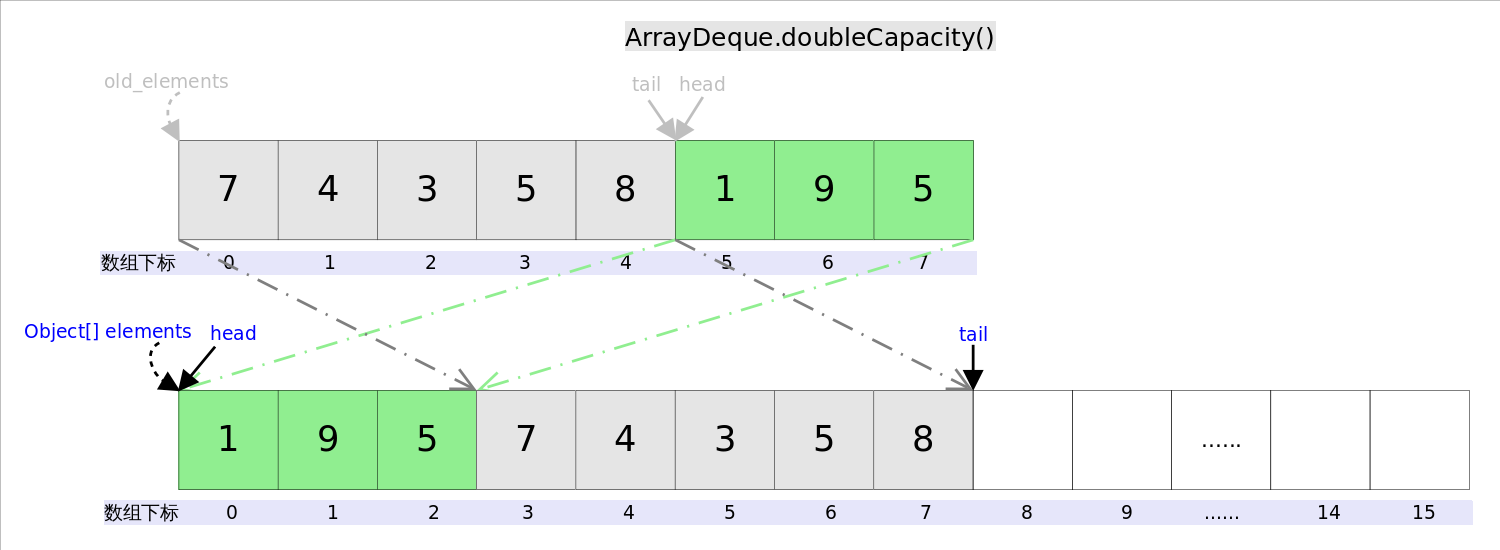
图中我们看到,复制分两次进行,第一次复制head右边的元素,第二次复制head左边的元素。
//doubleCapacity()
private void doubleCapacity() {
assert head == tail;
int p = head;
int n = elements.length;
int r = n - p; // head右边元素的个数
int newCapacity = n << 1;//原空间的2倍
if (newCapacity < 0)
throw new IllegalStateException("Sorry, deque too big");
Object[] a = new Object[newCapacity];
System.arraycopy(elements, p, a, 0, r);//复制右半部分,对应上图中绿色部分
System.arraycopy(elements, 0, a, r, p);//复制左半部分,对应上图中灰色部分
elements = (E[])a;
head = 0;
tail = n;
}
addLast()
addLast(E e)的作用是在Deque的尾端插入元素,也就是在tail的位置插入元素,由于tail总是指向下一个可以插入的空位,因此只需要elements[tail] = e;即可。插入完成后再检查空间,如果空间已经用光,则调用doubleCapacity()进行扩容。

public void addLast(E e) {
if (e == null)//不允许放入null
throw new NullPointerException();
elements[tail] = e;//赋值
if ( (tail = (tail + 1) & (elements.length - 1)) == head)//下标越界处理
doubleCapacity();//扩容
}
下标越界处理方式addFirt()中已经讲过,不再赘述。
pollFirst()
pollFirst()的作用是删除并返回Deque首端元素,也即是head位置处的元素。如果容器不空,只需要直接返回elements[head]即可,当然还需要处理下标的问题。由于ArrayDeque中不允许放入null,当elements[head] == null时,意味着容器为空。
public E pollFirst() {
E result = elements[head];
if (result == null)//null值意味着deque为空
return null;
elements[h] = null;//let GC work
head = (head + 1) & (elements.length - 1);//下标越界处理
return result;
}
pollLast()
pollLast()的作用是删除并返回Deque尾端元素,也即是tail位置前面的那个元素。
public E pollLast() {
int t = (tail - 1) & (elements.length - 1);//tail的上一个位置是最后一个元素
E result = elements[t];
if (result == null)//null值意味着deque为空
return null;
elements[t] = null;//let GC work
tail = t;
return result;
}
peekFirst()
peekFirst()的作用是返回但不删除Deque首端元素,也即是head位置处的元素,直接返回elements[head]即可。
public E peekFirst() {
return elements[head]; // elements[head] is null if deque empty
}
peekLast()
peekLast()的作用是返回但不删除Deque尾端元素,也即是tail位置前面的那个元素。
public E peekLast() {
return elements[(tail - 1) & (elements.length - 1)];
}